распределения давления в жидкости, времени схлопыванияи т

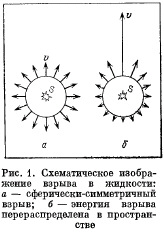
распределения давления в жидкости, времени схлопыванияи т. д. Оказалось, что при стремлении радиуса пузырькак нулю скорость поверхности пузырька и максимальноедавление в жидкости неограниченно возрастают.Бесконечные скорость и давление, конечно, не соответствуютдействительности: они получаются только в теории,где используется упрощенная модель кавитационногопроцесса.Теория Рэлея, несмотря на ее ограниченность, сыгралаважную роль в понимании физической сущности кавитации.Она показала, что при схлопывании кавитационныхпузырьков развиваются громадные давления, в сотнии тысячи раз превышающие атмосферное. Эти давленияпорождают в жидкости ударные волны. Ударная волнабыстро затухает по мере удаления от схлопнувшегосяпузырька. Однако если рядом с пузырьком находитсяповерхность твердого тела, достигающая ее ударная волнаимеет достаточную интенсивность, чтобы деформироватьэту поверхность. В зоне кавитации, как уже отмечалось,обычно возникает и захлопывается огромное количествопузырьков. Поэтому одна и та же область твердоготела испытывает многократно повторяющиеся импульсымеханического напряжения, которые приводят к усталостии последующему разрушению этой области.Попробуем «на пальцах» представить себе причину появлениябольших давлений в жидкости при схлопываниикавитационного пузырька. Нетрудно сообразить, что времясхлопывания пузырька тем больше, чем больше егопервоначальный радиус г, плотность жидкости р и чемменьше давление в жидкости р 0 вдали от пузырька. Отдругих параметров в первом приближении это времядругих параметров в первом приближении это время