Апрель 4th, 2013
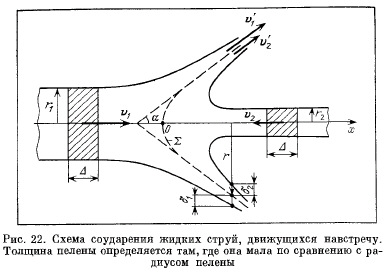
неограниченно уменьшается.Чтобы найти угол а при вершине конуса (см. рис. 22),рассмотрим взаимодействие двух участков обеих струйравной длины,Д = = v2t2, (2.6)где t± и t2 — промежутки времени, за которые жидкостив первой и второй струях соответственно проходят одинаковыерасстояния А. Закон сохранения импульса в проекциина ось х запишется в видеm1v1 — m2v2 = [m1v1 + m2v2)cos a , (2.7)где mx и m2 — массы участков длиной А соответственнопервой и второй струй. Так как объем участка А, например,первой струито из формулы (2.7) и аналогичного выражения для объемаучастка второй струи следует:ттгіУі + m2v2 (Pinr2 ) иг + v2Учитывая равенство (2.6), получаемВспоминая соотношение (2.2), последнее выражение можнопереписать в видеПолученная формула позволяет вычислить угол а конуса.Таким образом, поставленная задача полностью решена.§ 3. Пробивание струей прейятстйиЯ9 В задаче о соударении струй жидкости М. А. Лаврентьевувидел «готовую» гидродинамическую теорию кумулятивногоэффекта и путем несложных расчетов сумелопределить скорость и радиус кумулятивной струи, возникающейпри схлопывании конического углубления, атакже скорость и глубину проникновения струи в препятствие*Начнем с последней проблемы пробивания препятствиякумулятивной струей. Пусть тонкая металлическаяРис. 23. Схематическое изображение процесса пробивания металлическойструей препятствияструя (проволока) длиной I со скоростью и налетает наметаллическое препятствие цилиндрической формы(рис. 23, а), двигаясь по оси этого препятствия.
